Kontingenztabellen in R

Warum dieses Tutorial?

In der Explorativen Datenanalyse (EDA) ist die Untersuchung von Zusammenhängen zwischen Variablen eine der wichtigsten Aufgaben. Die Kontingenz- oder Kreuztabelle (contingency table) stellt die gemeinsame Häufigkeitsverteilung von zwei kategorialen Variablen dar.

HinweisHinweis

In diesem Tutorial lernen wir die Behandlung von Kontingenztabellen, sowohl mit der klassischen Base R, wie auch dem modernen Tidyverse.

Mathematische Beschreibung einer Kontingenztabelle (vgl. Mittag, Kapitel 9)

Eine Kontingenztafel für zwei diskrete Variablen/Merkmale \(X\) und \(Y\) lässt sich formal wie folgt darstellen:

\[ \begin{array}{l|cccccc|c} & b_1 & b_2 & \dots & b_j & \dots & b_m & \text{Summe} \\ \hline a_1 & h_{11} & h_{12} & \dots & h_{1j} & \dots & h_{1m} & h_{1\cdot} \\ a_2 & h_{21} & h_{22} & \dots & h_{2j} & \dots & h_{2m} & h_{2\cdot} \\ \vdots & \vdots & & \vdots & \ddots & & \vdots & \vdots \\ a_i & h_{i1} & h_{i2} & \dots & h_{ij} & \dots & h_{im} & h_{i\cdot} \\ \vdots & \vdots & & & & \ddots & \vdots & \vdots \\ a_k & h_{k1} & h_{k2} & \dots & h_{kj} & \dots & h_{km} & h_{k\cdot} \\ \hline \text{Summe} & h_{\cdot 1} & h_{\cdot 2} & \dots & h_{\cdot j} & \dots & h_{\cdot m} & n \\ \end{array} \]

Hierbei sind die Merkmale \((X, Y)\) mit ihren Ausprägungen (=Kategorien (engl. levels) der kategorialen Variablen) für \((X)\) die \((a_i)\) respektive für \((Y)\) die \((b_i)\). Wir nennen die Häufigkeiten dieser Paarungen bivariate Häufigkeitsverteilung. Die Randhäufigkeiten \(h_{\cdot j}\) bzw. \(h_{i \cdot}\) entsprechen den Zeilen- bzw. Spaltensummen.

Schauen wir gleich ein konkretes Beispiel an, damit wir uns nicht in den Notationen der Statistik verlieren.

Praxisbeispiel aus dem Softwareprojektmanagement:

Ist die Agile- oder die Wasserfall(waterfall)-Methodik in der Softwareentwicklung erfolgreicher?

Für 200 Softwareprojekte, die entweder nach der Agilen- oder Wasserfallmethodik durchgeführt wurden, sie nach Abschluss des Projekts die Entwicklerinnen und Entwickler befragt worden, ob die Projekte entweder erfolgreich oder herausfordernd (im Sinn von, schwierig umzusetzen) waren. Diese Daten wurden in zwei kategorialen Variablen Methode und Erfolg gespeichert und im csv software_projektdaten.csv gespeichert. Wir importieren ihn und definieren mit factor() aus der tidyverse Library die Variablen als kategoriale. Dies ist oft notwendig, weil dies bei einem Import aus einem csv häufig als String (chr) importiert werden. Man kann dies auch direkt bei einem Import über das Import Dataset Fenster in der Vorschau von RStudio der Daten durch wenige Klicks festlegen. Wir machen es hier nach dem Import. Die kategorialen Variablen haben hier nur zwei Klassen (levels):

• Methode: Agile, Wasserfall
• Erfolg: Erfolgreich und Herausfordernd

Aufgabe 1: Setup in R und Import der Daten

library(tidyverse)

# Import ohne Unterordner-Pfad, da wir im selben Verzeichnis schreiben
data_projekte <- read_csv("data/software_projektdaten.csv", show_col_types = FALSE)

# Faktoren definieren für korrekte Sortierung
data_projekte <- data_projekte %>%
  mutate(
    Methode = factor(Methode, levels = c("Agile", "Wasserfall")),
    Erfolg = factor(Erfolg, levels = c("Erfolgreich", "Herausfordernd"))
  )
glimpse(data_projekte)

Rows: 200
Columns: 2
$ Methode <fct> Wasserfall, Wasserfall, Agile, Wasserfall, Wasserfall, Agile, …
$ Erfolg  <fct> Herausfordernd, Herausfordernd, Erfolgreich, Herausfordernd, H…

head(data_projekte)

# A tibble: 6 × 2
  Methode    Erfolg        
  <fct>      <fct>         
1 Wasserfall Herausfordernd
2 Wasserfall Herausfordernd
3 Agile      Erfolgreich   
4 Wasserfall Herausfordernd
5 Wasserfall Herausfordernd
6 Agile      Erfolgreich   

Aufgabe 2: Erstellung der Kontingenztabellen

Um die Kontingenztabelle zu erstellen, müssen wir zählen, wie häufig die möglichen Paarungen auftreten können in einem Projekt, d.h. (Agile/Erfolgreich), (Agile/Herausfordernd), (Wasserfall/Erfolgreich), Wasserfall/Herausfordernd). Für die sogenannten Randsummen zählen wir wie häufig die einzelnen Kategorien Agile, Wasserfall, Erfolgreich und Herausfordernd auftreten. Wir schauen uns dies sowohl in Base R wie auch im tidyversean. Beginnen wir mit Base R.

a) Base R Weg:

Hier verwenden wir die Funktion table(). Diese erzeugt ein spezielles “table”-Objekt. Dies ist sehr kompakt für die schnelle Ansicht in der Konsole.

# Einfache Kreuztabelle
abs_table_base <- table(data_projekte$Methode, data_projekte$Erfolg)
abs_table_base

            
             Erfolgreich Herausfordernd
  Agile               82             26
  Wasserfall          45             47

# Randsummen hinzufügen
addmargins(abs_table_base)

            
             Erfolgreich Herausfordernd Sum
  Agile               82             26 108
  Wasserfall          45             47  92
  Sum                127             73 200

b) Tidyverse Weg: count() & pivot_wider()

Im Tidyverse zählen wir zuerst mit count() für beide Variablen, wie häufig die Kategorien vorkommen. Mit pivot_wider() gehen wir dann vom long zum wide Format (vergleich das Tutorial von Prof. Mike Chapple zum Data Wrangling mit R) Die Randsummen hinzuzufügen ist etwas aufwendiger als mit Base R, wie wir gleich sehen werden:

tabelle_breit <- data_projekte %>%
  count(Methode, Erfolg) %>%
  pivot_wider(names_from = Erfolg, values_from = n)

# Zeilensumme hinzufügen (Randverteilung von X)
tabelle_breit <- tabelle_breit %>%
  mutate(Summe_Erfolg = rowSums(across(where(is.numeric))))

# Spaltensumme hinzufügen (Randverteilung von Y)
tabelle_komplett <- tabelle_breit %>%
  bind_rows(
    tabelle_breit %>%  
      summarise(across(where(is.numeric), sum)) %>%
      mutate(Methode = "Summe Methode")
  )
tabelle_komplett

# A tibble: 3 × 4
  Methode       Erfolgreich Herausfordernd Summe_Erfolg
  <chr>               <int>          <int>        <dbl>
1 Agile                  82             26          108
2 Wasserfall             45             47           92
3 Summe Methode         127             73          200

Damit haben wir nun die gleiche Kontingenztabelle wie mit Base R. Der Vorteil liegt jedoch darin, dass wir mit dieser in der Variablen tabelle_komplett bei der späteren Visualisierung viel besser arbeiten können.

Aufgabe 2.1: Relative Häufigkeiten (Gesamtanteil)

Die Frage nach den relativen Häufigkeiten ist die Frage nach dem **Anteil jeder Kombination am Gesamt-n*?

Relative Häufigkeiten (vgl. Mittag 9.1)

\[ f_{ij} := f(a_i, b_j) = \frac{h(a_i, b_j)}{n} = \frac{h_{ij}}{n} \quad i = 1, 2, . . . , k;\quad j = 1, 2, . . . , m \]

Mit R berechnen wir:

Base R:

tab_rel <- addmargins(prop.table(abs_table_base))
tab_rel

            
             Erfolgreich Herausfordernd   Sum
  Agile            0.410          0.130 0.540
  Wasserfall       0.225          0.235 0.460
  Sum              0.635          0.365 1.000

• Innen: (\(f_{ij} = h_{ij}/n\)) (gemeinsame relative Häufigkeiten)
• Rechts/Unten: (\(f_{i\cdot}\)) und (\(f_{\cdot j}\)) (relative Randhäufigkeiten)
• Unten rechts: (1.00)

WarnungVorsicht: Zwei Anwendungen von prop.table(), die oft verwirren (und warum)

Fall 1: Zeilensummen hinzufügen und dann prop.table()

prop.table(addmargins(abs_table_base, 1))
           
             Erfolgreich Herausfordernd
  Agile             0.20           0.07
  Wasserfall        0.09           0.14
  Sum               0.29           0.21

Fall 2: Spaltensummen hinzufügen und dann prop.table()

prop.table(addmargins(abs_table_base, 2))

             Erfolgreich Herausfordernd  Sum
  Agile             0.20           0.07 0.27
  Wasserfall        0.09           0.14 0.23

Was passiert hier? Die Zahlenwerte sind nicht gleich, wie in der Gesamttabelle! prop.table(x) teilt jede Zelle durch die Gesamtsumme aller Einträge von x (also durch sum(x)). Wenn Sie mit addmargins() Randzeilen oder Randspalten hinzufügen, dann werden diese Summen zusätzliche Einträge in der Tabelle. Damit ändert sich der Nenner:

• Bei addmargins(abs_table_base, 1) wird eine Summe-Zeile hinzugefügt. Die Summe aller Einträge wird zu (2n) (Originalzellen: (n) + Summe-Zeile: (n)). ⇒ Die Zellenwerte wirken „halbiert“.

• Bei addmargins(abs_table_base, 2) analog: Summe-Spalte ⇒ Gesamtsumme (2n). ⇒ Ebenfalls „halbierte“ Werte.

Merke: Wenn Sie Wahrscheinlichkeiten (relative Häufigkeiten) mit korrekten Rändern wollen, zuerst prop.table() und erst danach addmargins(). `

Tidyverse:

tabelle_rel <- tabelle_breit %>%
  mutate(across(where(is.numeric), ~ .x / 200))

tabelle_rel

# A tibble: 2 × 4
  Methode    Erfolgreich Herausfordernd Summe_Erfolg
  <fct>            <dbl>          <dbl>        <dbl>
1 Agile            0.41           0.13          0.54
2 Wasserfall       0.225          0.235         0.46

Mathematisch korrekt aus den Randsummen berechnet:

Spalten: \[ f_{i\cdot} := \sum_{j=1}^{m} f_{ij} = \sum_{j=1}^{m}\frac{h_{ij}}{n} = \frac{h_{i\cdot}}{n}, \qquad i=1,\dots,k \] bzw.Zeilen: \[ f_{\cdot j} :=\sum_{i=1}^{k} f_{ij} = \sum_{i=1}^{k}\frac{h_{ij}}{n} = \frac{h_{\cdot j}}{n}, \qquad j=1,\dots,m \]

Dabei sind (\(h_{i\cdot}=\sum_{j=1}^m h_{ij}\)) und (\(h_{\cdot j}=\sum_{i=1}^k h_{ij}\)) die Randhäufigkeiten. Mit diesen relativen Häufigkeiten können wir die gemeinsamen (joint propabilities ) und bedingten (conditional propabilities) Wahrscheinlichkeiten schätzen.

Aufgabe 3: Gemeinsame und bedingte Wahrscheinlichkeiten:

Jetzt überlegen wir uns, wie wir z.B. \(P(\text{Erfolg} \cap \text{Methode})\) oder \(P(\text{Erfolg}|\text{Methode})\) aus relativen Häufigkeiten berechnen können.

In diesem Block haben wir Wahrscheinlichkeiten und bedingte Wahrscheinlichkeiten kennengelernt. Nach der frequentistischen Vorstellung von Laplace können wir mit den relativen Häufigkeiten aus der Kontingenztabelle die zugehörigen Wahrscheinlichkeiten abschätzen. So können wir z.B. aus den Randsummen die Wahrscheinlichkeit schätzen, dass ein beliebig gezogenes Projekt Agile durchgeführt wurde:

\[ P(\text{"Agile"}) \approx \frac{h_{1\cdot}}{n}= \frac{108}{200} \approx 0.54 \]

Gleiches gilt für die inneren Zellen der Kontingenztabelle. Wir können z.B. \(P(\text{"Erfolgreich"} \cap \text{"Agile"})\) berechnen:

\[ P(\text{"Erfolgreich"} \cap \text{"Agile"}) = \frac{h_{11}}{n} \approx \frac{82}{200} \approx 0.41 \]

Für die ganze Kontingenztabelle der relativen Häufigkeiten bedeutet das:

Die Wahrscheinlichkeitstabelle (gemeinsame und Randwahrscheinlichkeiten (Joint & Marginal Probabilities))

Die relativen Häufigkeiten als Schätzung der gemeinsamen und marginalen oder Randwahrscheinlichkeiten, können wir die Kontingenztabelle uns nun so vorstellen:

• Zellen im Inneren(z.B. \(P(A\cap B)\)): Dies sind die gemeinsamen Wahrscheinlichkeiten. Sie geben an, wie wahrscheinlich es ist, dass ein Projekt beide Eigenschaften gleichzeitig besitzt.
• Randsummen: Dies sind die Randwahrscheinlichkeiten (marginal probabilities) z.B. \(P(A)\). Sie entstehen durch Summation der Zeilen bzw. Spalten.
• Die 1 unten rechts: Sie repräsentiert das sichere Ereignis (100 %), da die Summe aller möglichen Merkmalskombinationen immer 1 ergeben muss.

\[ \begin{array}{l|c|c||c} \text{Methode} \setminus \text{Erfolg} & \text{Erfolgreich } (E) & \text{Herausfordernd } (H) & \text{Randwahrscheinlichkeit} \\ \hline \text{Agile } (A) & P(A \cap E)= 0.410 & P(A \cap H) = 0.140 & P(A) = 0.54 \\ \hline \text{Wasserfall} (W) & P(W \cap E)= 0.225 & P(W \cap H)=0.235 & P(W)=0.46 \\ \hline \hline \text{Randwahrscheinlichkeit} & P(E) = 0.635 & P(H) = 0.365& 1 \end{array} \] Nun interessieren wir uns noch für die bedingten Wahrscheinlichkeiten, die wir mit Hilfe der Kontingenztabelle schätzen können. Z.B. die Wahrscheinlichkeit, dass ein Projekt, welches mit der agilen Methode durchgeführt wurde erfolgreich war \(P(\text{"Erfolgreich"|"Agile"})\). Dies berechnet sich nach Definition aus:

\[ P(E|A) = \frac{P(E \cap A)}{P(A)} \approx \frac{82/200}{108/200} \approx 0.759 \]

Alle bedingten Wahrscheinlichkeiten im Überblick: \[ \begin{array}{l|cc||c} \textbf{1) Bedingung Methode} & \text{Erfolgreich }(E) & \text{Herausfordernd }(H) & \text{Summe} \\ \hline \text{Agile }(A) & P(E\mid A)=\frac{0.410}{0.540}\approx 0.759 & P(H\mid A)=\frac{0.130}{0.540}\approx 0.241 & 1 \\ \text{Wasserfall }(W) & P(E\mid W)=\frac{0.225}{0.460}\approx 0.489 & P(H\mid W)=\frac{0.235}{0.460}\approx 0.511 & 1 \\ \hline\hline \textbf{2) Bedingung Erfolg} & \text{Agile }(A) & \text{Wasserfall }(W) & \text{Summe} \\ \hline \text{Erfolgreich }(E) & P(A\mid E)=\frac{0.410}{0.635}\approx 0.646 & P(W\mid E)=\frac{0.225}{0.635}\approx 0.354 & 1 \\ \text{Herausfordernd }(H) & P(A\mid H)=\frac{0.130}{0.365}\approx 0.356 & P(W\mid H)=\frac{0.235}{0.365}\approx 0.644 & 1 \\ \end{array} \]

Was lernen wir daraus? Wir interessieren uns in der Praxis dafür, wie sich die Auswahl der Methode auf den Erfolg hat. Hier sehen wir einen deutlichen Unterschied. Während agile Projekte eine geschätzte Erfolgswahrscheinlichkeit von ca. 76 % aufweisen, liegen Wasserfall-Projekte deutlich darunter (ca. 49 %). Der zweite Teil der Tabelle mit Bedingung Erfolg wäre die Frage, mit welcher geschätzten Wahrscheinlichkeit ein erfolgreiches Projekt Agil oder Wasserfall ist? Das ist meist weniger interessant.

TippZwischenfazit: Was lernen wir aus Kontingenztabellen?

• Kontingenztabellen sind das Standardwerkzeug, um Zusammenhänge zwischen kategorialen Variablen in der EDA sichtbar zu machen (z. B. Methode () Erfolg).
• Aus absoluten Häufigkeiten (h_{ij}) werden über relative Häufigkeiten (f_{ij}=h_{ij}/n) Schätzungen von gemeinsamen und Randwahrscheinlichkeiten.
• Mit bedingten Wahrscheinlichkeiten (z. B. (P(EA))) beantworten Sie die zentrale Praxisfrage: Wie verändert sich die Erfolgsquote unter einer bestimmten Bedingung?

Aufgabe 4: Visualisierung der Ergebnisse

Um die geschätzten Wahrscheinlichkeiten zu visualisiern, nutzen wir zwei verschiedene Ansätze.

Aufgabe 4.1 Der 100 % gestapelte Barplot (Fokus: Bedingte Wahrscheinlichkeiten)

Dieser Plot ist die direkte visuelle Entsprechung zu unseren Berechnungen der bedingten Wahrscheinlichketien. Indem wir die Balken auf 100 % skalieren, eliminieren wir den Effekt, dass wir mehr Agile als Waterfall-Projekte im Datensatz haben. Wir vergleichen rein die Erfolgsquote.

ggplot(data_projekte, aes(x = Methode, fill = Erfolg)) +
  geom_bar(position = "fill") +
  scale_y_continuous(labels = scales::percent) +
  scale_fill_manual(values = c("Erfolgreich" = "skyblue", "Herausfordernd" = "#e74c3c")) +
  labs(
    title = "Bedingte Wahrscheinlichkeit: Erfolg gegeben Methode",
    subtitle = "Vergleich der Erfolgsquoten (P(E|A) vs. P(E|W))",
    x = "Projektmethodik",
    y = "Anteil in Prozent",
    fill = "Projektausgang"
  ) +
  theme_minimal()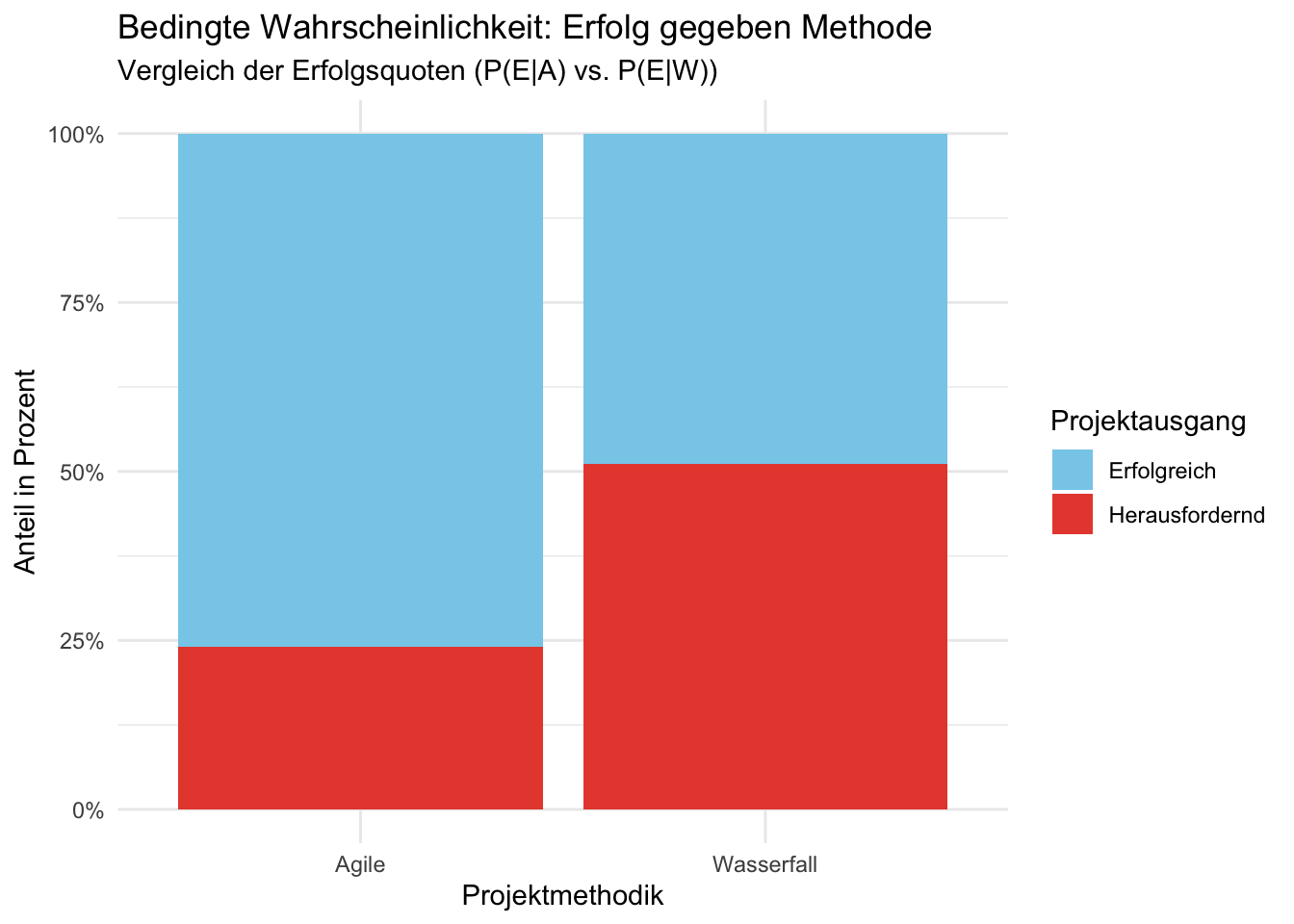

Interpretation: Hier sehen wir deutlich, dass der hellblaue Bereich bei “Agile” ca. 76 % des Balkens ausmacht, während er bei “Wasserfall” nur knapp unter 50 % liegt. Wenn wir also eine Projektmethode wählen, dann haben wir bei der agilen Methode eine viel höhere Erfolgswahrscheinlichkeit als beim traditionellen Wasserfall. Wir visualisieren also die Erfolgswahrscheinlichkeit unter der Bedingung der gewählten Methode.

Aufgabe 4.2 Der Mosaik-Plot (Fokus: Gemeinsame & Randwahrscheinlichkeiten, Bonus )

Der Mosaik-Plot ist die “Königsdisziplin”, da er die gesamte Kontingenztabelle abbildet.

• Die Breite der Balken zeigt die Randwahrscheinlichkeit (Man sieht, dass Agile breiter ist).
• Die Höhe der Segmente zeigt die zugehörige bedingte Wahrscheinlichkeit.
• Die Fläche eines Rechtecks entspricht der zugehörigen gemeinsamen Wahrscheinlichkeit .

# Wir nutzen hier die Basis-Funktion mosaicplot(), da sie sehr stabil ist
mosaicplot(abs_table_base, 
           main = "Mosaik-Plot: Methode vs. Erfolg",
           xlab = "Methode", 
           ylab = "Erfolg",
           color = c("skyblue", "#e74c3c"),
           border = "white")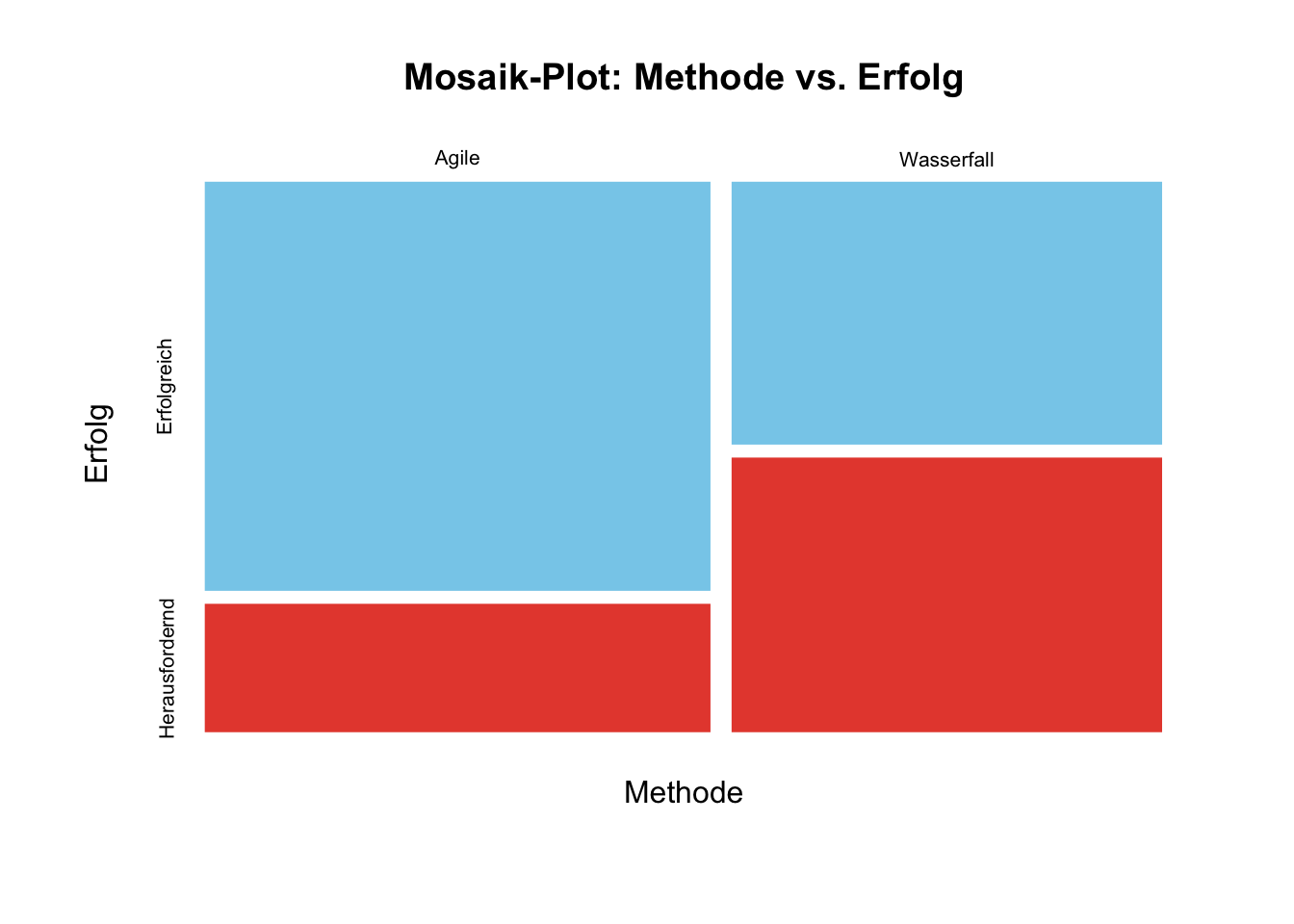

Hier sehen wir anhand der Breite der Teilbalken noch, dass es mehr Agile als Wasserfall-Projekte gegeben hat, diese also überrepräsentiert waren.

Zusammenfassung Visualisierung

Diagrammtyp	Was lerne ich daraus?	Mathematischer Bezug
100% Barplot	Welche Methode ist “effizienter”?	Bedingte Wahrscheinlichkeit
Mosaik-Plot	Wie verteilen sich alle 200 Projekte insgesamt?	Gemeinsame Wahrscheinlichkeit

Tipp: Wenn die Gruppen (Agile vs. Wasserfall) sehr unterschiedlich groß wären (z. B. 190 zu 10), würde der Mosaik-Plot dies durch einen extrem schmalen Balken sofort entlarven, während der 100% Barplot dies “verstecken” würde. Deshalb ist es immer gut, beide Perspektiven zu kennen.